Deskriptive Statistik in der Bachelorarbeit – Grundlagen
Deskriptive Statistik gehört zum Bereich der deskriptiven Forschung. Sie ist immer dann möglich, wenn quantitative Daten zu einem Thema vorliegen. Mit Hilfe der deskriptiven Statistik werden Stichproben hinsichtlich ihrer Struktur beschrieben und analysiert. Dieses Vorgehen steht im Unterschied zur Inferenzstatistik, bei der aus den Stichprobenergebnissen auf Regelmäßigkeiten in der Grundgesamtheit geschlossen wird.
In der deskriptiven Statistik wird mit verschiedenen Darstellungsformen gearbeitet. Mit Hilfe von Tabellen und Grafiken wird über die gesamte Verteilungsform informiert. Die Daten können Sie selbst erfassen oder von Datenbanken abrufen. Über Statista bekommen Sie zahlreiche Marktdaten und Kennzahlen. Wenn uns zum Beispiel die Altersverteilung von Nutzern des Smartphone-Bankings interessiert, dann finden wir hierzu die neuesten Studien. Die Ergebnisse lassen sich herunterladen und wir können in einer Tabelle z.B. so darstellen:
Anteil der Smartphone-Banking-Nutzer nach Altersgruppen in Deutschland in den Jahren 2021 bis 2023 | | |
| 2022 (n=779) | 2023 (n=763) |
16-29 Jahre | 78 % | 89 % |
30-49 Jahre | 67 % | 81 % |
50-64 Jahre | 65 % | 83 % |
Ab 65 Jahre | 50 % | 60 % |
Grafisch lassen sich die gleichen Daten folgendermaßen wiedergeben:
Weitere Methoden für die deskriptive Statistik in der Bachelorarbeit
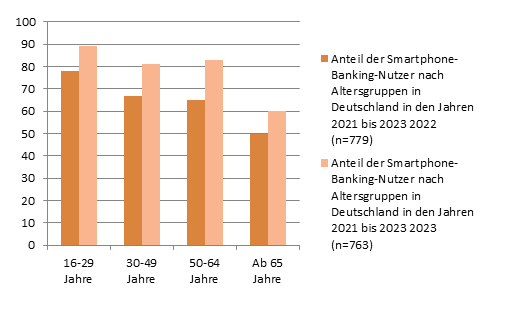
Die Nutzung von bereits vorliegenden Daten hat den Vorteil, dass Sie sich nur um die Daten selbst kümmern müssen. Datenbereinigung, -transformation und –codierung sind dann schon gemacht. Neben der Nutzung von Datenbanken haben Sie aber auch die Möglichkeit, eigene Daten zu erheben und z.B. mit SPSS auszuwerten. Deskriptive Statistik bezieht sich auf quantitative Daten. Qualitative Daten, wie Sie sie z.B. durch Interviews gewinnen, werden interpretativ ausgewertet.
Eine geeignete Methode der Datengewinnung für die deskriptive Statistik ist die Umfrage. Hierzu gibt es Tools, die Sie beim Erstellen der Fragebögen nutzen können. Gern unterstützen Sie aber auch unsere Ghostwriter. Sie können Hilfe für die Umfrage anfordern oder den Statistikteil einer Bachelorarbeit schreiben lassen.
Eigene Datenerhebung
Sie können eine deskriptive statistische Analyse auch mit eigenen Daten durchführen. Das hat den Vorteil, dass Sie genau die Daten erheben können, die Sie für die Beantwortung Ihrer Forschungsfrage brauchen. Je präziser die Daten sind, umso besser kann Ihre Analyse und Beschreibung der Zusammenhänge und Häufigkeiten ausfallen. Es ist daher unabdingbar, dass Sie die Datenerhebung gut planen. Aufbau und Ablauf der Untersuchung sollten bereits vor Beginn der Untersuchung vorstrukturiert sein. Für die Datenerhebung sind folgende Punkte wichtig:
Auswahl der Variablen:
Variablen haben immer mindestens zwei Abstufungen (wie etwa beim Geschlecht: männlich – weiblich). Die unabhängigen Variablen sind diejenigen Merkmale, deren Auswirkungen auf andere Merkmale (die abhängigen Variablen) untersucht werden.
Entscheidung für eine Art der Studie:
Sie können eine Labor- oder eine Felduntersuchung vornehmen. Laboruntersuchungen haben den Vorteil, dass äußere Störeinflüsse weitgehend ausgeschlossen werden können. Der Nachteil eines solchen Settings ist allerdings, dass die Ergebnisse nur bedingt generalisiert werden können.
Operationalisierung der Variablen:
Welche Operationen (Handlungen, Reaktionen usw.) wollen Sie als Anzeichen für die zu messenden Variablen ansehen? Wie wollen Sie die Variablen erfassen?
Festlegen der Stichprobengröße:
Wie viele Fälle Sie einbeziehen müssen, um belastbare Daten zu erhalten, gehört zu den schwierigsten Fragen in der Statistik. Im Rahmen einer Bachelorarbeit können Sie natürlich nur eine begrenzte Zahl von Daten sammeln. Dennoch muss natürlich sichergestellt sein, dass Ihre Ergebnisse verallgemeinerbar sind. An diesem Punkt kann Unterstützung durch professionelles Ghostwriting sinnvoll sein. Unsere Ghostwriter haben Zugriff auf die wichtigsten Datenbanken und können Ihnen dabei helfen, relevante Daten als Grundlage für Ihre deskriptive Statistik zu finden. Gern können Sie unsere kostenlose Fragebogen-Vorlage verwenden und für Ihre Zwecke ändern. Unsere Ghostwriter können Ihnen auch helfen, eigene Daten zu erheben.
Planung der statistischen Auswertung:
Schon bevor Sie die Daten erheben, sollten Sie sich Gedanken über die spätere Auswertung machen. SPSS ist kostenpflichtig und nicht so leicht zu bedienen. Statistische Auswertungen sind auch mit Hilfe von Excel möglich.
Welche Datentypen gibt es?
Statistische Daten werden auf Skalen dargestellt, die auch als Messniveau bezeichnet werden. Für die statistische Auswertung in der Bachelorarbeit kommen drei Typen von Daten in Frage, nämlich nominale, ordinale und metrische Daten.
Nominaldaten
Nominaldaten sind Werte aus Kategorien, die sich nicht in eine natürliche Reihenfolge bringen lassen. Hierzu zählen z.B. Wohnort, Postleitzahl oder Religionszugehörigkeit. Bei nominalen Daten werden nur die Ausprägungen unterschieden, aber es gibt keine Bezüge zwischen den einzelnen Werten. Wenn Sie mit Nominaldaten arbeiten, müssen Sie sich vorher einige Gedanken machen, wie Sie die Daten darstellen. Am besten besprechen Sie das vorher mit Ihrem Betreuer. Die Experten von GWriters können Sie ebenfalls unterstützen, wenn Sie Statistikhilfe in der Bachelorarbeit brauchen.
In unserem Beispiel mit den Klausurnoten wären Nominaldaten beispielsweise Hobbys der Studenten. Sie können die Freizeitbeschäftigungen erfassen und in einen Bezug zu den Klausurnoten setzen. Allerdings sind die Bezüge nicht so eindeutig, wie z.B. bei metrischen Daten. Hierbei handelt es sich um Daten, die sich nach Intervallen skalieren lassen. In unserem Beispiel könnten wir die Studiendauer zum Zeitpunkt der Klausur erfassen oder die Vornote.
Ordinaldaten
Auch Ordinaldaten lassen sich eindeutig darstellen. Hierbei handelt es sich um Werte aus Kategorien mit einer natürlichen Reihenfolge. Klassischerweise ergeben sich Ordinaldaten aus Zustimmungswerten auf einer Skala. Solche Werte werden bei Einstellungsmessungen und Präferenzbeurteilungen erfasst. Ordinaldaten lassen sich nach den Ausprägungen sortieren, etwa die Abstufungen von „sehr zufrieden“ bis „sehr unzufrieden“.
Statistik Bachelorarbeit für viele Fachgebiete nötig
Ob Sie in der Abschlussarbeit ein statistisches Thema bearbeiten, können Sie in hohem Maße mitentscheiden. Grundsätzlich spielen statistische Fragen in vielen Fachgebieten eine Rolle, weshalb entsprechende Grundkenntnisse unabdingbar sind. Mögliche Bachelorarbeit Statistikthemen könnten sein.
Welche Werte sind in der deskriptiven Statistik relevant?
In der deskriptiven Statistik sind v.a. die so genannten Lage- und die Streuungsmaße von Bedeutung. Zu den Lagemaßen bzw. Lageparametern zählen Modus (oder Modalwert), Median, arithmetisches, geometrisches und harmonisches Mittel sowie die Quantile. Die wichtigsten Streuungsmaße sind die Spannweite, der Quartilsabstand, die mittlere absolute Abweichung, die Varianz und Standardabweichung sowie der Variationskoeeffizient.
Beispiel für eine deskriptive Statistik
Was diese Werte im Einzelnen bedeuten, wird am besten in einem konkreten Beispiel deutlich. Für eine fiktive Bachelorarbeit wählen wir für die statistische Auswertung das Beispiel einer Klausur, bei der die folgenden Noten gegeben wurden:
Note | Anzahl der Studenten |
Note 1 | 1 Student |
Note 2 | 4 Studenten |
Note 3 | 12 Studenten |
Note 4 | 8 Studenten |
Note 5 | 2 Studenten |
Note 6 | 1 Student |
N = 28, es haben also Studenten die Klausur mitgeschrieben.
Lagemaße |
Maß | Bedeutung | Beispiel |
Modus bzw. Modalwert | Der häufigste Wert, der in der Stichprobe vorkommt | Der Modus oder Modalwert ist in diesem Falle die Note 3. |
Median | Der Median teilt die Werte in zwei Teile. Wenn alle Werte geordnet werden, ist der Median der Wert in der Mitte. Wenn es eine gerade Anzahl von Werten gibt (wie in unserem Beispiel), dann ist der Median der Mittelwert aus den beiden Werten in der Mitte. | Der Median ist in unserem Beispiel 10 (Mittelwert aus 12 und 8). |
Arithmetisches Mittel | Der Durchschnitt aus allen Werten, ein anderer Begriff ist empirischer Mittelwert. | Das arithmetische Mittel ist 4,667 (Gesamtwert = 28 : Anzahl = 6) |
geometrisches Mittel | Die n-te Wurzel (n = Anzahl der Daten, die vorliegen) aus dem Produkt der vorliegenden Daten, ein anderer Begriff ist mittlere Proportionale. | Das geometrische Mittel ist 1,743. (6. Wurzel aus28) |
harmonisches Mittel | Der Mittelwert einer Menge von Zahlen, entspricht dem arithmetischen Mittel der Kehrwerte. | Das harmonische Mittel beträgt 0,471. (6: (1:1+1:4+1:12+1:8+1:2+1:6)) |
Empirisches Quantil | Das empirische Quantil teilt die Stichprobe in Werte, die jeweils größer und die kleiner sind, anderer Begriff: Stichprobenquantil | (diese Größe ist in unserem Beispiel nicht relevant) |
Streuungsmaße |
Spannweite | Die Spannweite gibt die Abweichung zwischen den größten und dem kleinsten Messwert wieder. | In unserem Beispiel beträgt die Spannweite 11. (größter Messwert = 12 – kleinster Messwert = 1). |
Quartilsabstand | Der Quartilsabstand gibt an, wie breit das Intervall ist, in dem sich 50% der Stichprobenelemente befinden, andere Begriffe: Interquartilsabstand, IQA oder IQR | Der Quartilsabstand ist 4 (12-8) |
mittlere absolute Abweichung | Die mittlere absolute Abweichung gibt an, wie weit eine Stichprobe im Mittel vom mittleren arithmetischen Mittel abweicht, anderer Begriff: MAD (mean absolute deviation) | Die mittlere absolute Abweichung beträgt 2. Hierfür gibt es einen Online-Rechner, der die MAD an Hand Ihrer Daten errechnet. |
Varianz und Standardabweichung | Die Varianz gibt das Maß der Wahrscheinlichkeitsdichte um den Schwerpunkt der Daten herum an. Von ihr ausgehend wird die Standardabweichung berechnet. | Die Varianz beträgt 110 und die Standardabweichung 10,488. Varianz = (1-6)2+(4-6)2+(12-6)2+(8-6)2+(2-6)2+(1-6)2 = 110 Standardabweichung: = 10,488 |
Variationskoeeffizient | Der Variationskoeeffizient gibt die relative Streuung an, also das prozentuale Verhältnis der Standardabweichung zum arithmetischen Mittel. | Der Variationskoeeffizient beträgt 1,0488: In diesem Beispiel haben wir Ihnen schon einmal erklärt, wie der Variationskoeffizient errechnet wird: Sie benötigen die Differenz aus Standardabweichung und Mittelwert, in unserem Beispiel also 10,488 : 10 = 1,0488 |
Zusammenhangsmaße wie z.B. der Korrelationskoeffizient oder die Kovarianz sind in der deskriptiven Statistik nicht bedeutsam. Diese Maße benötigen Sie in der analytischen Statistik.
Wie sieht die Interpretation der Ergebnisse aus?
Wenn Sie in Ihrer Bachelorarbeit eine deskriptive Statistik einbinden, ist die Interpretation der Ergebnisse wichtig. Hierfür sind fünf Schritte wichtig, die wir Ihnen an Hand unseres Bachelorarbeit Statistikbeispiels darstellen.
1. Schritt: Sie beschreiben zunächst den Stichprobenumfang
In unserem Beispiel haben 28 Studenten an der Klausur teilgenommen. Die Notenverteilung können wir z.B. mit einer Grafik darstellen. Die Diagramm-Tools von Excel reichen für diese Zwecke völlig aus.
2. Schritt: Sie stellen das Zentrum der Daten dar
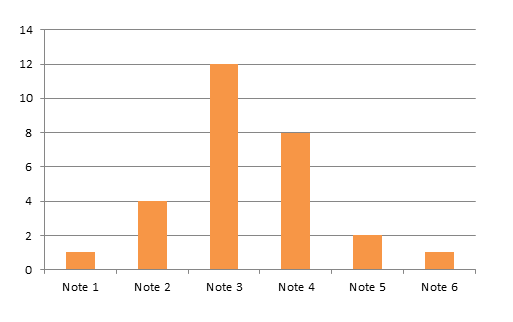
Anschließend beschreiben Sie das Zentrum der Daten. Hierfür benötigen Sie den Mittelwert oder den Median sowie die Standardabweichung. Diesen Zusammenhang können Sie tabellarisch darstellen, etwa so:
Modus | N (Anzahl) | Standardabweichung | Median |
3 | 28 | 10,488 | 10 |
Wichtig ist, dass Sie die Daten nicht nur als Zahlen darstellen, sondern sie auch beschreiben: Die Standardabweichung ist in unserem Beispiel sehr hoch, was daran liegt, dass die Noten sich über die gesamte Skala verteilen.
3. Schritt: Sie stellen die Streubreite der Daten dar
Im 3. Schritt steht die Streubreite der Daten im Fokus. Hierfür bietet sich ein Pareto-Diagramm an. Auch das lässt sich mit Excel leicht erstellen. Es würde für unsere Daten folgendermaßen aussehen:
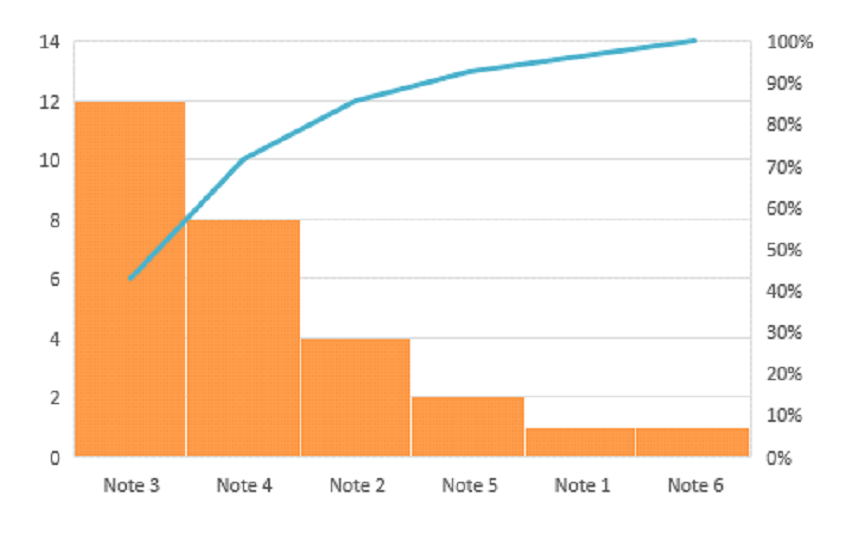
Im Pareto-Diagramm werden die Daten nach Häufigkeit klassifiziert. In unserem Beispiel werden von links in absteigender Reihenfolge die Noten mit der häufigsten Verteilung angezeigt.
Häufig werden auch Boxplots erstellt. Damit ist ebenfalls erkennbar, wie sich die Daten verteilen.
4. Schritt: Sie werten die Datenverteilung aus
Im nächsten Schritt müssen Form und Streubreite der Datenverteilung ausgewertet werden. Hierfür können Sie ein Säulendiagramm verwenden.
Sie sehen, dass unsere Daten linksschief verteilt sind. Das bedeutet, dass die Mehrheit der Daten sich auf der rechten Seite der Skala befindet. In unserem Falle heißt das, dass die Klausurergebnisse sehr schlecht ausgefallen sind.
5. Schritt: Sie vergleichen Daten aus verschiedenen Gruppen
Im letzten Schritt werden die Daten aus verschiedenen Gruppen verglichen. In unserem Beispiel könnten wir z.B. erfassen, wie sich die Klausurnoten nach Geschlechtszugehörigkeit oder nach Studiendauer verteilen.
Wenn wir die Klausurnoten mit der Studiendauer vergleichen, ergibt sich folgendes Bild:
Note | Studenten aus dem 1. Studienjahr | Studenten aus dem 2. Studienjahr |
Note 1 | 0 | 1 |
Note 2 | 1 | 3 |
Note 3 | 8 | 4 |
Note 4 | 7 | 1 |
Note 5 | 2 | 0 |
Note 6 | 1 | 0 |
Teilnahme an Klausur | 19 | 9 |
Es haben 19 Studenten aus dem ersten Studienjahr mitgeschrieben, gegenüber 9 aus dem zweiten Studienjahr. Grafisch lassen sich die Ergebnisse folgendermaßen darstellen:
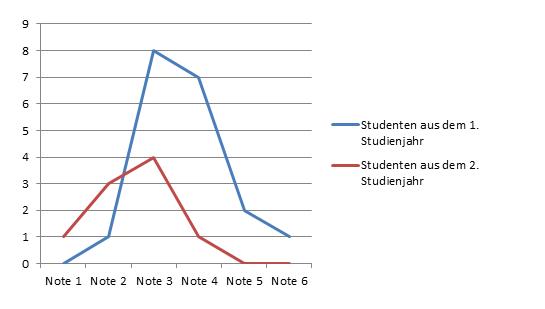
Die Streubreite der Noten bei den jüngeren Studenten ist leicht größer als bei den älteren Studenten. Auch in Bezug auf Standardabweichung und Median zeigen sich Unterschiede. Lediglich der Modus ist gleich: In beiden Gruppen wurde am häufigsten die Note 3 erzielt.
| Modus | N (Anzahl) | Standardabweichung | Median |
1. Studienjahr | 3 | 19 | 10,344 | 1,5 |
2. Studienjahr | 3 | 9 | 11,225 | 1 |
Eine weitere Größe, die wir in unserem Beispiel erfassen könnten, ist das Geschlecht der Studenten. Möglicherweise zeigen sich auch hier Unterschiede in den erzielten Noten.
Vor- und Nachteile einer deskriptiven Statistik in einer Bachelorarbeit
Der größte Vorteil einer deskriptiven Statistik in der Bachelorarbeit ist, dass Sie sich keine Sorgen machen müssen, wie Sie auf die vorgeschriebene Seitenzahl kommen. So lange Sie Daten haben, können Sie diese beschreiben und darstellen. Deskriptive Statistik liefert zudem einen Überblick, was bei größeren Datenmengen sinnvoll sein kann.
Allerdings sind für den Überblick fundierte Statistik-Kenntnisse nötig. Sie müssen die wichtigsten Lage- und Streumaße errechnen und erklären können. Das stellt für viele Studenten ein Problem dar. Viele greifen daher auf die Hilfe von professionellen Ghostwritern zurück. Die Experten von Gwriters können Ihnen bei der Datenbeschaffung genauso helfen wie bei der Darstellung der Ergebnisse. Ghostwriter kennen die Anforderungen für deskriptive statistische Analysen in der Bachelorarbeit, da sie über ein breites Grundwissen für Statistik verfügen und bereits viele Fallbeispiele für Bachelorarbeiten bearbeitet haben.
